by Calculated Risk on 10/06/2008 08:13:00 PM

Earlier today I posted the Q2 2008 home equity extraction data provided by the Fed's Dr. James Kennedy. This shows that equity withdrawal has fallen almost to zero as of Q2.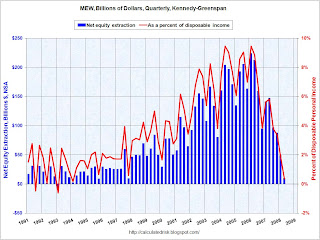

Click on graph for larger image in new window.

For Q2 2008, Dr. Kennedy has calculated Net Equity Extraction as $9.5 billion, or 0.3% of Disposable Personal Income (DPI).

Note: This data is based on the mortgage system presented in "Estimates of Home Mortgage Originations, Repayments, and Debt On One-to-Four-Family Residences," Alan Greenspan and James Kennedy, Federal Reserve Board FEDS working paper no. 2005-41.

Equity extraction was close to $700 billion per year in 2004, 2005 and 2006, before declining to $471 billion last year and will probably be less than $100 billion in 2008.

The questions are: how much will this impact consumption? And over what period?

Unfortunately there is no clear answer. Fed Chairman Bernanke has argued that falling house prices, not equity extraction, impacts consumption (from the WSJ in 2007):

"Our sense ... is that consumers respond to changes in the value of their home essentially because there’s a change in their wealth, not because there’s a change in their access to liquid assets."
...
Mr. Bernanke went on to reiterate it’s the price of homes, not MEW or financial contagion that represents the biggest risk of spillover from the housing slump. ... [H]e said a hit to consumer spending could be expected on the order of “4 cents and 9 cents on the dollar” of lost home wealth.

Others place more weight on MEW. Since equity withdrawal is a somewhat recent development, and there are many factors that impact consumption, it is hard to develop a predictive model on the impact of MEW on consumption. Equity withdrawal probably started in earnest with the Tax Reform Act of 1986 that eliminated the interest deduction for credit cards and consumer loans.

In an Economic Letter in 2006, Fed economist John V. Duca wrote:

We can think of the overall impact of home prices on consumption as the combination of two parts—the traditional wealth effect and the relatively new and growing phenomenon of mortgage equity withdrawal (MEW). In recent years, U.S. households have been extracting housing wealth through home-equity loans, cash-out mortgage refinancings or by not fully rolling over capital gains from sales into down payments on subsequent home purchases. Because home-equity loans and mortgages are collateralized, they usually carry lower interest rates than unsecured loans; thus, homeowners can borrow more cheaply. Also, by making housing wealth more accessible, financial innovations have opened new avenues for families to act more quickly on their consumption preferences.

Consistent with a growing liquidity, or MEW effect, some new studies have found wealth effects are now greater than earlier research suggested. One estimates that a $100 rise in housing wealth leads to a $9 increase in spending. Another finds that increases in housing wealth generate three times the spending from stock-price gains. Neither study, however, directly examines whether housing wealth has a greater impact on consumption today because of the greater ease of accessing home equity.
...
The limited U.S. econometric evidence indicates that the strong pace of MEW may have boosted annual consumption growth by 1 to 3 percentage points in the first half of the present decade. This implies that a slowing of home-price appreciation into the low single digits might shave 1 to 2 percentage points off consumption growth and 0.75 to 1.5 percentage points from GDP growth for a few years.

While these estimates provide an idea of housing’s potential economic impact, considerable uncertainty exists about how much a slowdown in MEW might restrain consumption growth.

Duca didn't mention the impact of falling house prices.

As far as when the impact occurs, on the wealth effrect, Carroll, Otsuka, and Slacalek, How Large Is the Housing Wealth Effect? A New Approach October 18, 2006 suggested that the impact would be over several quarters:

[W]e estimate that the immediate (next-quarter) marginal propensity to consume from a $1 change in housing wealth is about 2 cents, with a final long run effect around 9 cents.

For MEW, it is also uncertain. Kennedy and Greenspan tried to quantify the data in Sources and Uses of Equity Extracted from Homes, however:

Our results do not provide an estimate of the [marginal propensity to consume (MPC)] out of housing wealth; nor do they address the question as to whether extraction of housing wealth has an effect on PCE in addition to the standard wealth effect.

My guess is that the MEW effect lasts over several quarters (only a guess). Greenspan estimated that approximately 50% of MEW is consumed, and in interviews he suggested it is probably consumed over several quarters. Since MEW was $471 billion in 2007, and will probably be under $100 billion in 2008, we can estimate that half of the $400 billion or so decline in MEW (or $200 billion) is the drag on PCE in 2008 from less MEW.

That is a big number, but to put that in perspective, PCE increased over $500 billion from 2007 to 2008. So nominal PCE will increase in 2008, although consumption will probably slow sharply.

PCE will also be impacted by lost jobs and changes in consumer psychology (all the scary news will probably lead to less consumer spending).

Nearly six out of ten Americans believe another economic depression is likely, according to a poll released Monday.

The CNN/Opinion Research Corp. poll, which surveyed more than 1,000 Americans over the weekend, cited common measures of the economic pain of the 1930s:

25% unemployment rate;

widespread bank failures; and

millions of Americans homeless and unable to feed their families.

So once again it will be difficult to separate out the various factors impacting consumption. This will probably be an area of significant econometric research over the next few years.

It does appear that real personal consumption expenditures declined in Q3 2008 for the first time since 1991. And some of that decline is probably related to the decline in MEW.