by Tanta on 12/29/2007 02:15:00 PM

This is a bonus post for those of you who use Excel (or some other software with which you can read and play with .xls files). I'm afraid that those of you who do not possess such software will have to use your imagination here. It's not especially practical to post images of big spreadsheets on the blog, so if you want to see the numbers, you'll need to download the spreadsheets.

These links will download the spreadsheets:

LIBOR-Indexed OA Projection

MTA-Indexed OA Projection

I made two of them for you to play with. Both show a to-date balance history, plus a future balance projection, for a hypothetical Option ARM with payments beginning in 2002, 2003, 2004, 2005, 2006, or 2007. The loan terms are identical for each spreadsheet with the exception of the index chosen: one uses MTA, the other 1-Month LIBOR. The terms of these scenarios are in fact derived from real loan products out there, but of course there are other ways of structuring OAs. I am not making a claim about what product structure was most common (or most likely still to be on the books), as I don't have that kind of data.

What I had in mind for this exercise is to help people see, clearly, how these things work (some folks are still, Lord love you, a bit confused about OA mechanics. That undoubtedly includes some of you who have one. Remember that if you do, your loan might not work like this because the note you signed might have different terms regarding adjustment frequency, balance cap, margin, etc.) Besides that, I wanted to make a fairly simple point about the issue of resets, payment shock, and timing on these things.

That's why the spreadsheets show multiple vintages with identical loan terms: you can see that the actual speed of negative amortization and the forecast date of recast on these loans varies quite dramatically for the vintages, because of the huge impact of the very low 2002-2003 rate cycle. Each of these scenarios assumes that the borrower always makes the minimum payment from inception of the loan, and each assumes that future index values are identical to the most recent available index value (December 2007). Yet even in those circumstances, the earlier loans (2002 and 2003, especially) negatively amortize much more slowly than the later vintages.

My gifted co-blogger has actually created some lovely charts to help make that clear: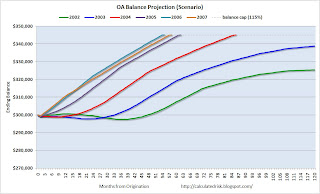

Click on graph for larger image.

If you've downloaded the spreadsheets, you can play around with them a little in terms of the future interest rates on these loans, and you can see how the recast date (the date the balance hits the balance cap and the loan payment must be recast to fully amortize over the remaining term) moves forward or back depending on what you do with the rates. This is one reason why modeling actual portfolios of OAs is such a challenge: you have to make assumptions about what will happen with the underlying index.

Of course, in actual portfolio modeling, you would also not assume that every borrower will always make the minimum payment. You would have to look at actual borrower performance to date, and calculate some "average" behavior or project each borrower's past behavior patterns into the future. I am not making the claim that all borrowers always make the minimum payment from inception; I'm trying to show what would happen, in some examples, if a borrower did that. I have heard estimates from different OA portfolios of anywhere from one-third to ninety percent of borrowers who have, historically, done that.

One other thing I wanted to make clear by providing these examples is the mechanics of payment increases for a very common OA type. The product shown in these spreadsheets allows for annual payment increases, but monthly rate increases. (That is how the potential for negative amortization gets created: the payment does not automatically adjust to match the new interest rate each month.) The eventual recast hits at the sooner of the loan reaching 115% of its original balance or 120 months. We know that a recast is nearly always a huge shock, given a low enough introductory rate. But this loan does involve payment increases of up to 7.5% each year (i.e., the next year's payment can be as much as 107.5% of the prior year's payment).

With the later vintage loans, especially, I for one have no confidence that the borrower was qualified at realistic enough original DTIs to withstand several years of payment increases, even before that nasty shock of the recast.

You may if you like change that introductory rate on these loans--I used 1.00%. You will see that increasing that introductory rate actually slows down the negative amortization in most scenarios. (That is because it creates a higher initial first year payment, which thus creates less of a shortfall between interest accrued and payment made.) I suspect that this fact about OA is surprising to some people, who think that folks who got a 1.00% "teaser" on these things got some real deal. In reality, a borrower who was given an introductory rate several points higher than that is probably doing much better, balance-wise.

My scenarios involve the assumption that the initial payment is fixed for only one year. There are OAs out there where the first payment change is two or even up to five years from the first payment date. (They will generally involve a higher introductory rate and margin.) You can change these spreadsheets to extend the original payment out for longer than a year, if you like, and you'll see just how much faster that balance cap hits when you extend the fixed payment period. Ouch.

Finally, while I chose the repayment periods I did quite arbitrarily, you will notice that for both the MTA and LIBOR scenarios, the most recent index value (December 2007) is substantially lower than it had been for quite some time. This means that my balance forecast here just happens to have picked up a relatively low last known index to project out into the future. Had we done this exercise several months ago, the projected future index value would have been higher, and hence the future negative amortization would have been faster. It's an issue to keep in mind as we look at portfolio and security projections regarding OA recasts; those will have to be updated from time to time as rate history unfolds.

And yes, there's a pig, if that makes you want to bother downloading the spreadsheets.